【導讀】時間交錯技術可使用多個相同的模數(shù)轉(zhuǎn)換器[1] (ADC),并以比每一個單獨數(shù)據(jù)轉(zhuǎn)換器工作采樣速率更高的速率來處理常規(guī)采樣數(shù)據(jù)序列。簡單說來,時間交錯(IL)由時間多路復用M個相同的ADC并聯(lián)陣列組成,如圖1所示。這樣可以得到更高的凈采樣速率fs(采樣周期Ts = 1/fs),哪怕陣列中的每一個ADC實際上以較低的速率進行采樣(和轉(zhuǎn)換),即fs/M。因此,舉例而言,通過交錯四個10位/100 MSPS ADC,理論上可以實現(xiàn)10位/400 MSPS ADC。
為了更好地理解IL原理,圖1中一個模擬輸入VIN (t)以M個ADC進行采樣,其結(jié)果為組合數(shù)字輸出數(shù)據(jù)序列DOUT。ADC1最先采樣VIN (t0)并開始將其轉(zhuǎn)換為n位數(shù)字信號。Ts秒后,ADC2將采樣VIN (t0+Ts)并開始將其轉(zhuǎn)換為n位數(shù)字信號。接著,Ts秒后,ADC3將采樣VIN (t0 +2Ts),以此類推。ADCM完成VIN (t0 +(M-1)×Ts)采樣后,開始下一個采樣周期,并從ADC1采樣VIN (t0 +M×Ts)開始,依次進行下去。
由于ADC順序輸出n位數(shù)據(jù)且輸出順序與剛才描述的采樣操作順序一致,這些數(shù)字n位字由同一張圖右側(cè)的解復用器所采集。這里獲取的是重新組合的數(shù)據(jù)輸出序列DOUT (t0 + L),DOUT (t0 + L + Ts),DOUT (t0 + L + 2Ts),...。L表示每一個單獨ADC的固定轉(zhuǎn)換時間,而該重新組合的數(shù)據(jù)序列是一個n位數(shù)據(jù)序列,采樣速率為fs。因此,雖然各個ADC(通常稱為"通道")為n位ADC且采樣速率為fs/M,但整體等于采樣速率為fs的單個n位ADC,而我們將其稱為時間交錯ADC(與通道相區(qū)別)。輸入本質(zhì)上是分隔開的,并由陣列中的ADC單獨處理,然后在輸出端連續(xù)重組,以便構(gòu)成輸入VIN的高數(shù)據(jù)速率表示DOUT。
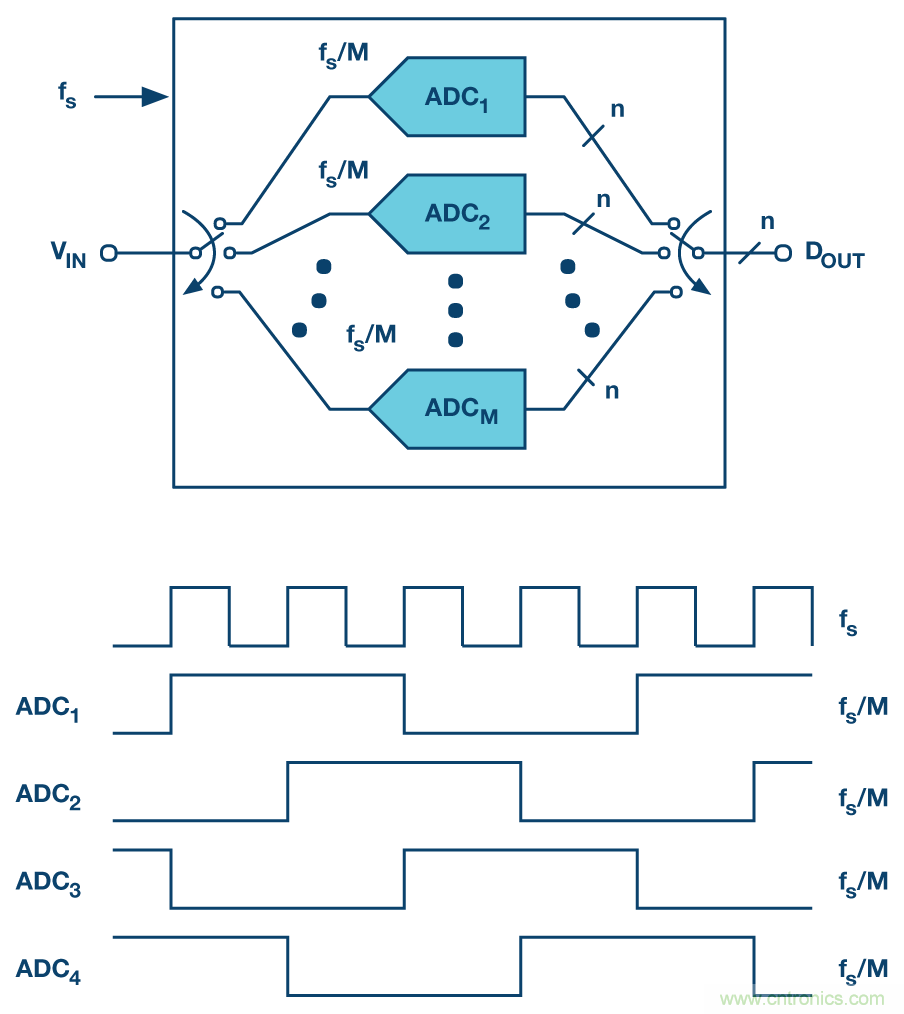
圖1. M次交錯的n位ADC陣列每一個ADC的采樣速率為fs/M,得到的時間交錯ADC采樣速率為fs。M = 4的時鐘方案示例在該圖下半部分顯示。
這種強大的技術在實際使用時存在一些難題。一個重要的問題是來自通道的M數(shù)據(jù)流經(jīng)過數(shù)字組裝后重構(gòu)原始輸入信號VIN。如果我們看一下頻譜DOUT;除了看到VIN的數(shù)字信號以及模數(shù)轉(zhuǎn)換引入的失真,我們還將看到額外的和大量的雜散成分,稱為"交錯雜散"(或簡稱為IL雜散);IL雜散既沒有多項式類型失真的簽名——比如較高次信號諧波(2次,3次,等等)——也沒有量化或DNL誤差簽名。IL偽像可視為時域固定碼噪聲的一種形式,由通道中的模擬損害引起,因為在交錯過程中采用分隔轉(zhuǎn)換信號進行調(diào)制并出現(xiàn)在最終的數(shù)字化輸出DOUT。
讓我們分析一個簡單的示例,了解可能會發(fā)生什么情況??紤]頻率fIN下正弦輸入VIN的雙路交錯ADC情況。假定ADC1具有增益G1,ADC2具有差分增益G2。在這種雙路IL ADC中,ADC1和ADC2將交替采樣VIN。因此,如果ADC1轉(zhuǎn)換偶數(shù)樣本,而ADC2轉(zhuǎn)換奇數(shù)樣本,則所有DOUT偶數(shù)數(shù)據(jù)的幅度都將由G1設置,而所有DOUT奇數(shù)數(shù)據(jù)的幅度都將由G2設置。然后,DOUT不僅包含VIN,還包括一些多項式失真,但它受到G1和G2的交替放大,就好像我們采用頻率為fs/2的方波對VIN進行幅度調(diào)制。這樣做會引入更多雜散成分。特別地,DOUT在fs/2 – fIN頻率處會包含"增益雜散";并且不幸的是,該雜散的頻率會跟蹤輸入fIN,且位于交錯ADC的第一奈奎斯特頻段內(nèi)(即在fs/2內(nèi)),而在所有其它奈奎斯特頻段內(nèi)也會存在混疊。該交錯雜散的功率/幅度取決于兩個增益G1和G2之間的凈差。換言之,它取決于增益誤差失配[2]。而最終,它取決于輸入VIN自身的幅度。
如果輸入并非簡單正弦波,而是真實應用中的全頻帶限幅信號,那么"增益雜散"就不只是干擾音了,而是頻帶限幅輸入信號自身的完整調(diào)節(jié)鏡像,出現(xiàn)在奈奎斯特頻段內(nèi)。這在一定程度上抵消了交錯帶來的帶寬增加的優(yōu)勢。
雖然上例中我們僅考慮了通道間的增益誤差失配,其它損害也會引起交錯雜散。失調(diào)失配(通道失調(diào)之間的差)引起固定頻率的信號音("失調(diào)雜散"),功率與失調(diào)失配成正比[3]。當某些通道比預定順序更早或更晚采樣某位時,便發(fā)生采樣時間偏斜。它會引入"時間雜散",其頻率與增益雜散完全一致(并疊加同樣的幅度)[4]但功率會隨著fIN的增加以及輸入幅度的增加而不斷加強。各通道之間的帶寬失配會引入更多的雜散成分,頻率取決于fIN,并且正如時間雜散,雜散功率不僅隨著輸入幅度,而且還會隨著fIN自身而逐步增加。再次強調(diào),無論何種情況,輸出頻譜下降的程度并不取決于通道損害的絕對值(失調(diào)、增益、時序、頻段),而是取決于通道之間的相對失配或通道之差。
雖然時間交錯的基本技術存在已有幾十年,但IL可在何種程度上保持最小化則將其過去的適用性限制于低分辨率轉(zhuǎn)換器。然而,最近在通道失配校準方面以及抑制殘留IL雜散成分方面的進步已經(jīng)可以實現(xiàn)全集成、極高速、12/14/16位IL ADC。
這種情況下,我們需要對交錯進行分類。我們一般將兩個交錯通道稱為"乒乓"工作。然后,當我們描述較少通道數(shù)的情況(比如3通道至4通道),以及大量通道的情況時(比如超過4個通道,通常達到8個或更多),我們還區(qū)分了"輕度交錯"和"重度交錯"。
乒乓(雙路)交錯
當我們只是交錯兩個通道以便使采樣速率翻倍時,我們將其稱為"乒乓",如圖2 (a)中的框圖所示。這是一種最簡單的情況,它有一些有趣和有用的特性。這種情況下,在交錯ADC的第一奈奎斯特頻段內(nèi),交錯雜散位于直流、fs/2和fs/2 – fIN處。因此,如果輸入信號VIN是一個對中至fIN的窄帶信號——如圖2 (b)中的第一奈奎斯特輸出頻譜所示——交錯雜散包含直流處的失調(diào)雜散、fs/2處的另一個失調(diào)失配雜散以及對中至fs/2 – fIN的增益和時序雜散鏡像,看上去就像輸入自身的一個放大復制版本。
如果輸入信號VIN (f)完全位于0和fs/4之間——如圖2 (b)所示——那么交錯雜散不與數(shù)字化輸入頻率重疊。此時,壞消息是我們只能數(shù)字化半個奈奎斯特頻段,就好比只有一個時鐘為fs/2的單通道,雖然我們依舊消耗至少兩倍于該單個通道的功耗。奈奎斯特頻段上限的交錯雜散鏡像可在數(shù)字化之后通過數(shù)字濾波手段抑制,無需進行模擬損害校正。
但好消息是由于乒乓ADC時鐘為fs,數(shù)字化輸出得益于動態(tài)范圍內(nèi)的3 dB處理增益。此外,與使用時鐘為fs/2的單個ADC相比,乒乓ADC放寬了抗混疊濾波器設計要求。
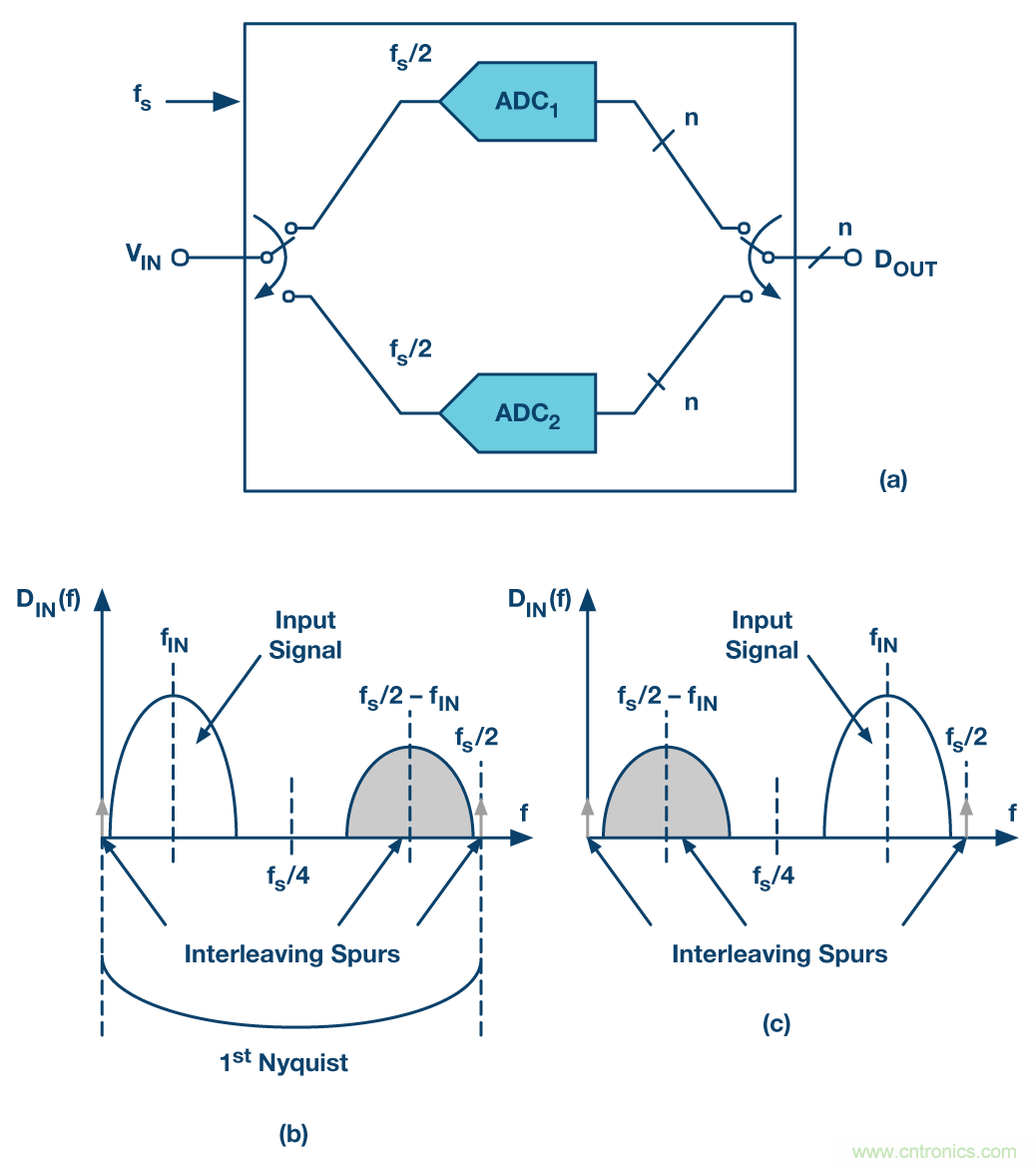
圖2. (a)乒乓方案(b)窄帶輸入信號位于fs/4以下時的輸出頻譜(c)此時輸入信號位于fs/4和奈奎斯特頻率fs/2之間。
如果窄帶信號位于第一奈奎斯特頻段的上半部,則所有考慮因素都適用,如圖2 (c)所示,因為交錯鏡像雜散移至奈奎斯特頻段的下半部分。再次強調(diào),增益和時序雜散可在濾波數(shù)字化之后通過數(shù)字手段抑制。
最后,輸入信號和交錯雜散的頻率將會重疊,并且一旦輸入信號頻率位置跨過fs/4線,交錯鏡像就會破壞輸入頻譜。這種情況下,恢復所需輸入信號將是不可能的,而乒乓方案不可用。當然,除非通道間匹配足夠緊密,使得交錯雜散成分對于應用來說達到可以接受的低程度,或者引入校準來降低導致IL鏡像的原因。
總之,頻率規(guī)劃和某些數(shù)字濾波可以恢復乒乓方案中的窄帶數(shù)字化輸入,哪怕存在通道失配。雖然轉(zhuǎn)換器功耗相比使用單個時鐘為fs/2的ADC時基本翻了個倍,但乒乓方案提供了3 dB處理增益,同時放寬了抗混疊要求。
采用乒乓方案并且無任何通道失配校正的一個示例,以及其產(chǎn)生的交錯雜散見圖3。在該例中,兩個雙通道14位/1 GSPS ADC AD9680以交替乘以正弦波的速率進行采樣,從而返回單個組合輸出數(shù)據(jù)流,速率為2 GSPS。當我們查看該乒乓方案輸出頻譜的第一奈奎斯特頻段時(位于直流和1 GHz之間),可以看到輸入音,它是fIN = 400 MHz時位于左側(cè)的強音;我們還能看到在fs/2 – fIN = 2G/2 – 400 M = 600 MHz處有較強的增益/時序失配雜散。由于通道本身的失真以及其它損害,我們還能看到一系列其它信號音,但都低于–90 dB線。
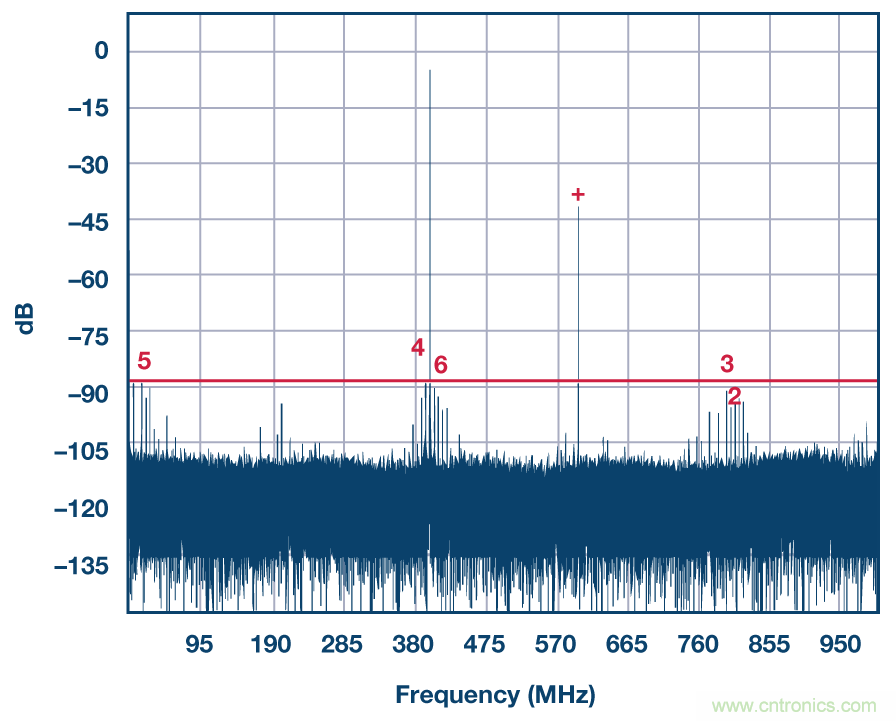
圖3. 乒乓方案的2 GSPS輸出數(shù)據(jù)組合頻譜,采用兩個AD9680在1 GSPS時鐘下獲取,采樣相移為180°。
更高次交錯
當具有兩個以上通道時,上文所說的頻率規(guī)劃就不那么實用了。我們無法將交錯雜散的位置限定在奈奎斯特頻段的某一小部分。比如考慮四路交錯ADC的情況,如圖4 (a)所示。此時,失調(diào)失配會提高直流、fs/4和fs/2時的信號音,而增益和時序交錯鏡像位于fs/4 – fIN、fs/4 + fIN和fs/2 – fIN。交錯ADC輸出頻譜的一個示例請參見圖4 (b)。很明顯,除非輸入位于fs/8以內(nèi)的帶寬之內(nèi),否則無論fIN的位置如何,輸入都會與部分交錯雜散重疊,并且如果輸入是一個極端窄帶信號,那么我們不應當嘗試使用寬帶交錯ADC將其數(shù)字化。
在這種情況下,我們需要最大程度降低IL雜散功率,以便獲得完整的奈奎斯特頻譜和更干凈的頻譜。為了達到這個目的,我們使用校準技術來補償通道間失配。校正失配的影響后,最終的IL雜散功率會下降。SFDR和SNR都會得益于該雜散功率的下降。
補償方法受限于失配可測量并最終校正的精度。除了校準所能達到的水平外,為了進一步抑制殘留雜散,還可間歇性隨機打亂通道輸入采樣的順序。這樣做之后,前面討論的由于未校準失配而產(chǎn)生的轉(zhuǎn)換輸入信號調(diào)制效果將從固定碼噪聲轉(zhuǎn)換為偽隨機噪聲。因此,IL音和干擾周期碼轉(zhuǎn)換為偽隨機噪聲類成分,并疊加至轉(zhuǎn)換器量化噪底而消失,或者至少將干擾雜散鏡像和信號音加以擴散。此時,與IL雜散成分有關的功率疊加至噪底功率。因此,雖然改善了失真,但SNR可能下降,下降量為IL雜散功率加上噪聲。SNDR (SINAD)基本上沒有變化,因為它由失真、噪聲和隨機化組成;它只是將IL貢獻因素從一個成分(失真)轉(zhuǎn)移到另一個成分(噪聲)。
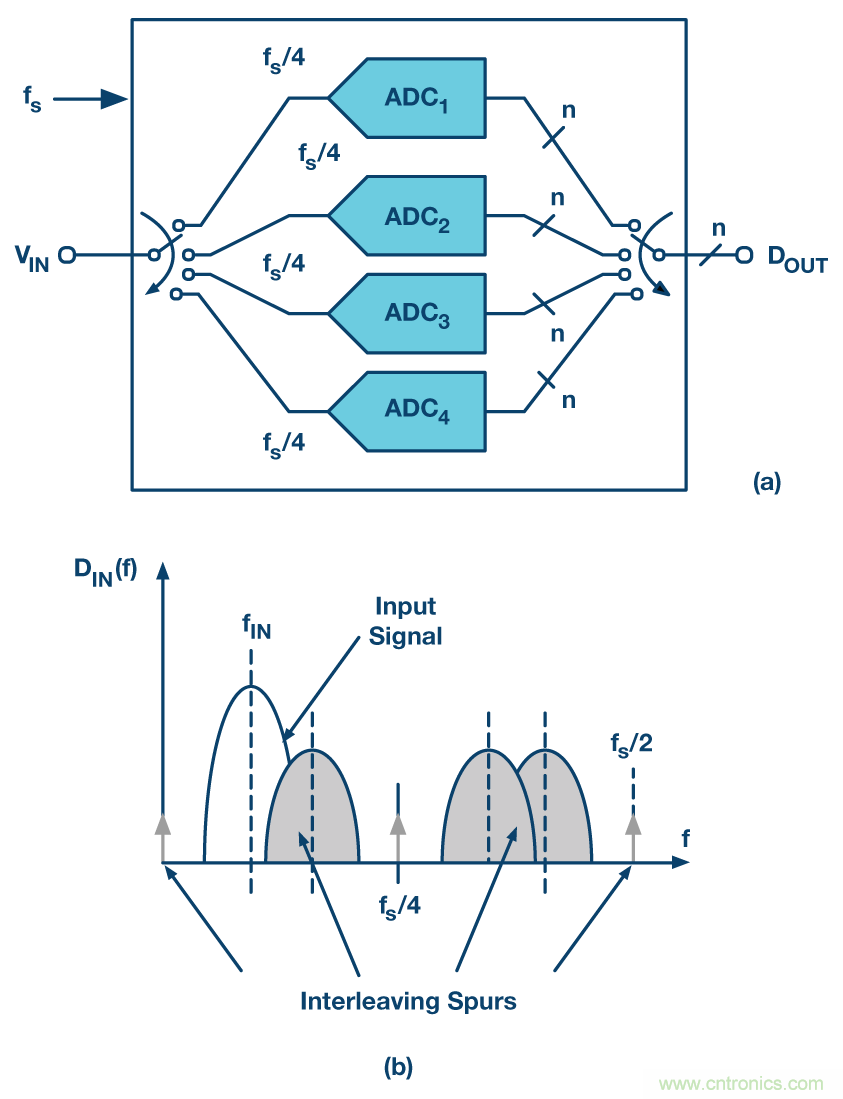
圖4. (a)四路交錯ADC (b)對應顯示交錯雜散的第一奈奎斯特輸出頻譜
讓我們來看幾個交錯ADC的示例。AD9625是一個12位/2.5 GSPS三路交錯ADC。對三個通道之間的失配進行校準,以便最大程度減少交錯雜散。圖5 (a)所示是一個輸入接近1 GHz的輸出頻譜示例。在該頻譜中,除了約為1 GHz的輸入音外,還可以看到通道在500 MHz附近存在2次和3次諧波失真,并在基頻處存在4次諧波失真。交錯失配校準可大幅降低交錯雜散的功耗,并且在整個頻譜中可以看到大量的額外殘留的較小雜散音。
為了進一步減少這些殘留雜散成分,引入了通道隨機化。加入了第四個校準通道,然后將四個通道變?yōu)槿方诲e,并通過間歇性將交錯通道與第四個更換,實現(xiàn)隨機改變順序。這就好比人們可以像耍雜技那樣將三根柱子投向空中,然后每一次都更換第四根。這樣做之后,可使殘留交錯雜散功率隨機化,然后擴散到噪底。如圖5 (b)所示,經(jīng)過通道隨機化之后,交錯雜散幾乎消失了,而噪聲功率卻只略為增加,因而SNR降低2 dB。當然,需要注意的是,雖然圖5 (b)中的第二個頻譜比失真音遠為干凈,但隨機無法影響2次、3次和4次諧波,因為這些諧波不是交錯雜散。
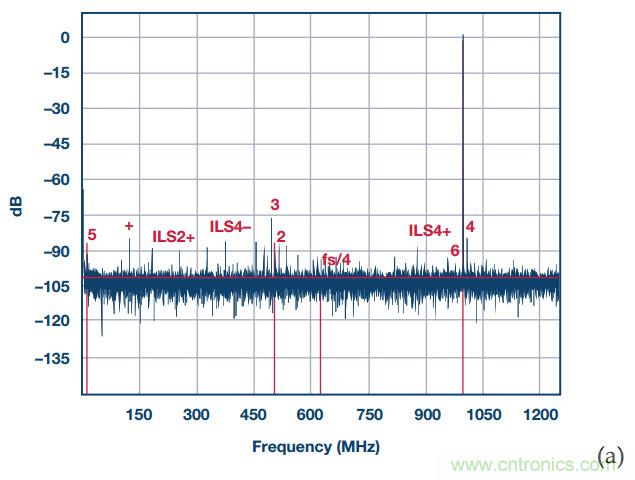
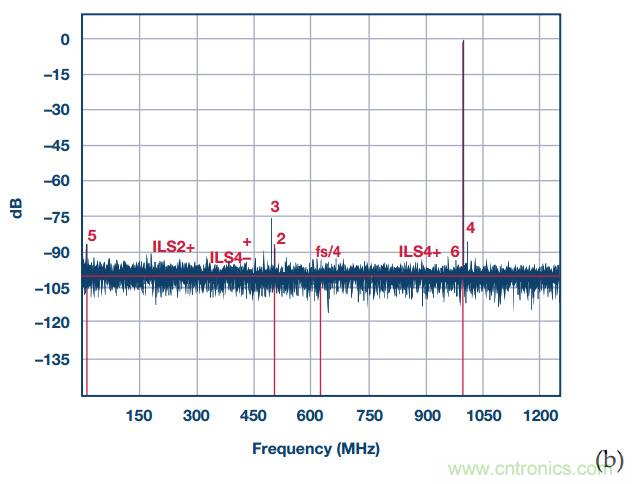
圖5. AD9625的輸出頻譜,時鐘為2.5 GSPS,輸入音接近1 GHz。(a)順序三路交錯;SNR = 60 dBFS,SFDR = 72 dBc,受限于3次諧波,接近500 MHz;然而,整個頻譜中可見大量交錯雜散。(b)三路交錯,隨機通道置亂;SNR = 58 dBFS,而SFDR = 72 dBc依然由3次諧波決定,通過將功率擴散到噪底而消除了所有交錯雜散。
使用通道隨機化的另一個交錯ADC示例如圖6中的頻譜所示。此時采用四路交錯16位/310 MSPS ADC AD9652。圖6示例中,四個通道以固定順序交錯,并且不進行任何減少通道失配的校準。頻譜清楚表明交錯雜散位于預計頻率位置,且它們的大功率遠高于2次和3次諧波,并將無雜散動態(tài)范圍限制為僅有57 dBc。
然而,如果同樣的ADC經(jīng)過前景校準以便減少通道失配,那么交錯雜散功率將會大幅下降,如圖7所示。與上例中的情況類似,通道諧波失真不受影響,但通過通道失配校準大幅降低了交錯雜散功率。
最后,圖7中的頻譜純度可得到進一步改善,方法是使通道順序隨機化,如圖8所示。此時,隨機化使用專利技術,對四個通道的順序進行間歇性加擾無需通過另一個(第五個)通道來達成,從而省下了與此相關的功耗。如圖8所示,經(jīng)過隨機化之后,結(jié)果頻譜中僅有常規(guī)諧波失真。
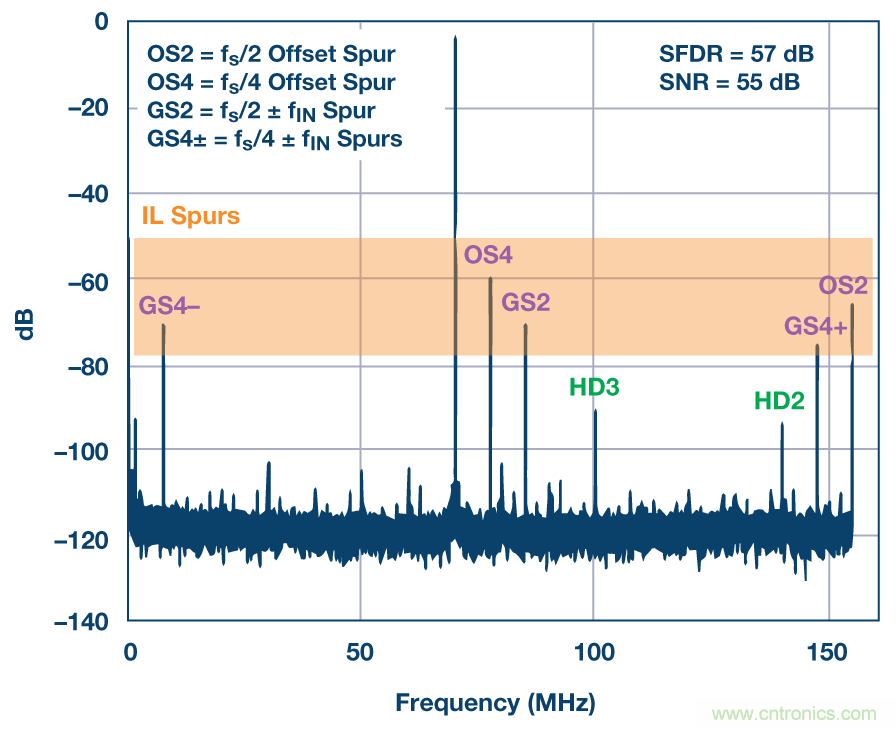
圖6. AD9652的輸出頻譜,時鐘為 fs=310 MHz,采用fIN ~70 MHz的正弦輸入。此時,未施加通道校準和隨機化。2次(HD2)和混疊3次(HD3)諧波分別在大約140 MHz和100 MHz處可見。交錯(IL)雜散同樣可見。這些是直流、fs/2(圖中的OS2)以及fs/4(圖中的OS4)處的失調(diào)音。另外,增益(時序)雜散可見于fs /2-fIN(圖中的GS2)、fs /4+fIN(圖中的GS4+)以及fs /4- fIN(圖中的GS4-)。此圖中的SNR查詢?nèi)藶樽儾盍?,因為部分雜散成分和噪聲功率混在了一起。
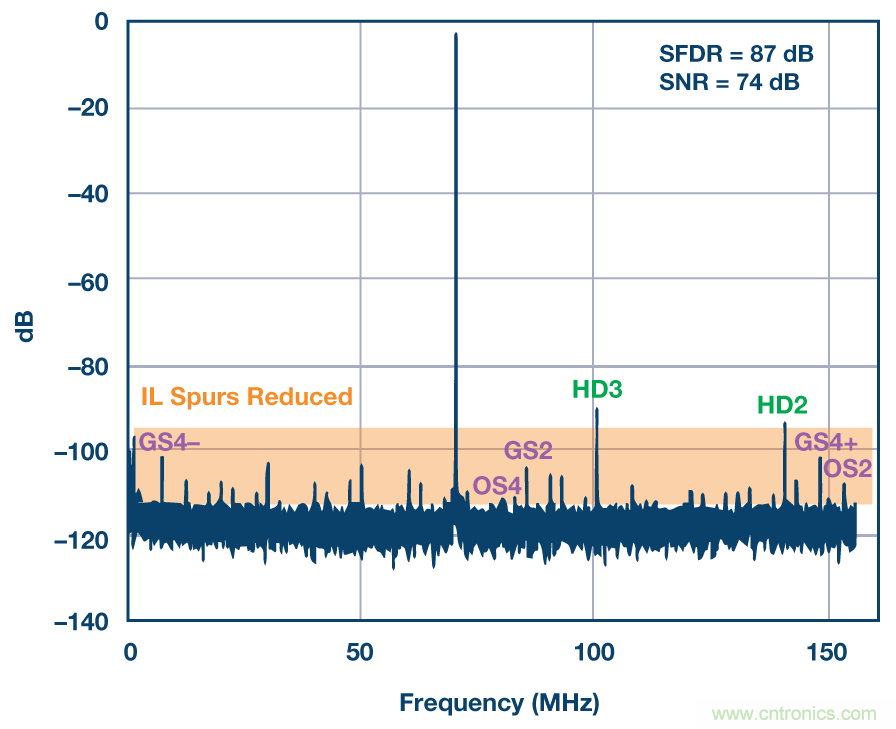
圖7. 同一個AD9652的輸出頻譜,采用同樣的輸入,但經(jīng)過校準后四個通道減少了失配。與圖6相比,雖然2次和3次諧波未受影響,但交錯雜散的功率大幅下降,并且SFDR改善了30 dB,即從57 dBc到87 dBc。
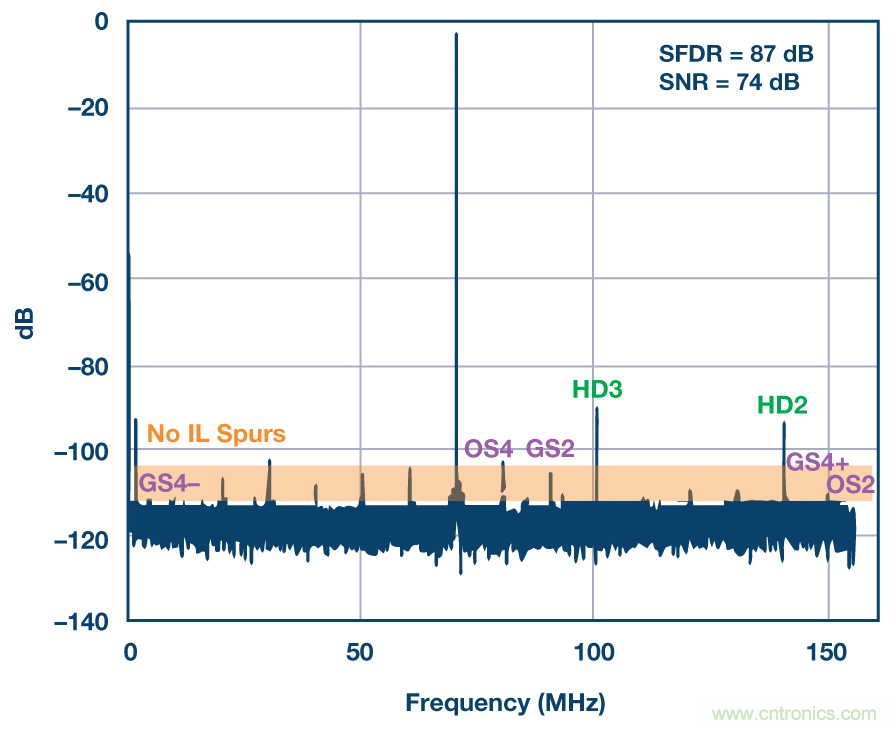
圖8. 上例開啟交錯順序隨機化之后的輸出頻譜。隨機化殘留交錯雜散可將它們的功率擴散到噪底中,相應的尖峰便消失了。可以看到的僅有常規(guī)諧波失真。SNR幾乎未受影響,因為來自交錯音并擴散的雜散功率經(jīng)過失配校準后可以忽略。
結(jié)論
時間交錯是增加數(shù)據(jù)轉(zhuǎn)換器帶寬的強大技術。最近在失配校準方面,以及通過隨機化技術消除殘留雜散成分方面的發(fā)展已經(jīng)能夠?qū)崿F(xiàn)完全集成、極高速12/14/16位交錯ADC。
在輸入信號受頻帶限制的情況下(比如很多通信應用),乒乓(雙路)交錯方法可通過頻率規(guī)劃將干擾交錯雜散分配到遠離目標輸入頻段的位置。然后便可以數(shù)字手段過濾雜散成分。雖然這種方法相比工作在IL采樣速率一半的非交錯式ADC獲得同樣的無雜散輸入帶寬所需的功耗要高出幾乎一倍,但它不僅可以通過處理增益提高動態(tài)范圍3 dB,而且還能降低抗混疊的滾降,并修平ADC前的濾波器——因為IL采樣速率高。
若需要用到IL轉(zhuǎn)換器的全部輸入頻帶才能捕捉寬帶輸入信號,那么可以采用更高次的交錯轉(zhuǎn)換器。這種情況下,校準和隨機置亂可實現(xiàn)交錯失真和雜散成分的補償和消除。
Endnotes
[1] 雖然此處僅討論了模數(shù)轉(zhuǎn)換器,但所有原理同樣適用于數(shù)模轉(zhuǎn)換器的時間交錯特性。.
[2] 請注意,重要的是增益誤差不匹配,而不是絕對值。因為如果兩個通道具有相同的增益(誤差),則G1 = G2。 這種情況下,兩個通道均同樣擴大,從而將兩個數(shù)據(jù)流重新整合到單一DOUT數(shù)據(jù)流中,而無需幅度(或調(diào)制)交替,且未引入增益雜散。
[3]一般而言,對于M通道交錯,fOS = (k/M) fS時會出現(xiàn)失調(diào)雜散,其中k = 0、1、2... (Manganaro, 2011年)。
[4]一般而言,對于M通道交錯,fGS = ± fIN + (k/M) fS時會出現(xiàn)增益和時序偏斜圖像,其中k = 1、2... (Manganaro, 2011年)。
參考電路
Beavers, Ian. “千兆采樣ADC通過快速運行應對新挑戰(zhàn)”,ADI公司,2014年。
Black, William and David Hodges. “時間交錯轉(zhuǎn)換器陣列” IEEE Journal of Solid-State Circuit,第SC-15卷第6期,1980年。
Bosworth, Duncan. “GSPS數(shù)據(jù)轉(zhuǎn)換器拯救電子監(jiān)控與對抗系統(tǒng)。”, ADI公司,2014年。
Elbornsson, Jonas, Fredrik Gustafsson, 和 Jan-Erik Eklund. “分析隨機交錯ADC系統(tǒng)中的失配影響” IEEE Transactions on Circuits and Systems, 第52卷第3期,2005年。
Harris, Jonathan. “深入了解交錯式ADC的本質(zhì).” EDN Network, 2013年.
Harris, Jonathan. “交錯式ADC入門” EDN Network, 2013.
Manganaro, Gabriele. Advanced Data Converters. Cambridge, UK: Cambridge University Press, 2011.
推薦閱讀:








